Implementation of PlanarFigure to display an angle through three control points. More...

#include <mitkPlanarAngle.h>

Inheritance diagram for mitk::PlanarAngle:

Collaboration diagram for mitk::PlanarAngle:

Public Types
typedef PlanarAngle	Self
typedef PlanarFigure	Superclass
typedef itk::SmartPointer< Self >	Pointer
typedef itk::SmartPointer < const Self >	ConstPointer
Public Member Functions
virtual const char *	GetClassName () const
unsigned int	GetMinimumNumberOfControlPoints () const
	Place figure in its minimal configuration (a point at least) onto the given 2D geometry.
unsigned int	GetMaximumNumberOfControlPoints () const
	Angle has 3 control points per definition.
Static Public Member Functions
static Pointer	New ()
Public Attributes
const unsigned int	FEATURE_ID_ANGLE
Protected Member Functions
	PlanarAngle ()
virtual	~PlanarAngle ()
virtual void	GeneratePolyLine ()
	Generates the poly-line representation of the planar figure.
virtual void	GenerateHelperPolyLine (double mmPerDisplayUnit, unsigned int displayHeight)
	Generates the poly-lines that should be drawn the same size regardless of zoom.
virtual void	EvaluateFeaturesInternal ()
	Calculates feature quantities of the planar figure.
virtual void	PrintSelf (std::ostream &os, itk::Indent indent) const

Detailed Description

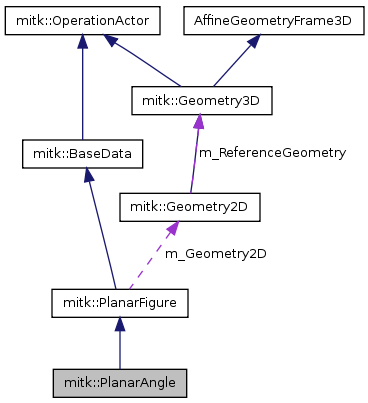
Implementation of PlanarFigure to display an angle through three control points.

Definition at line 35 of file mitkPlanarAngle.h.

Member Typedef Documentation

typedef itk::SmartPointer<const Self> mitk::PlanarAngle::ConstPointer

Reimplemented from mitk::PlanarFigure.

Definition at line 38 of file mitkPlanarAngle.h.

typedef itk::SmartPointer<Self> mitk::PlanarAngle::Pointer

Reimplemented from mitk::PlanarFigure.

Definition at line 38 of file mitkPlanarAngle.h.

typedef PlanarAngle mitk::PlanarAngle::Self

Reimplemented from mitk::PlanarFigure.

Definition at line 38 of file mitkPlanarAngle.h.

typedef PlanarFigure mitk::PlanarAngle::Superclass

Reimplemented from mitk::PlanarFigure.

Definition at line 38 of file mitkPlanarAngle.h.

Constructor & Destructor Documentation

mitk::PlanarAngle::PlanarAngle ( ) [protected]

Definition at line 23 of file mitkPlanarAngle.cpp.

References mitk::PlanarFigure::m_HelperPolyLines, mitk::PlanarFigure::m_HelperPolyLinesToBePainted, mitk::PlanarFigure::m_PolyLines, and mitk::PlanarFigure::ResetNumberOfControlPoints().

: FEATURE_ID_ANGLE( this->AddFeature( "Angle", "deg" ) )
{
  // Start with two control points
  this->ResetNumberOfControlPoints( 2 );

  m_PolyLines->InsertElement( 0, VertexContainerType::New());
  m_HelperPolyLines->InsertElement( 0, VertexContainerType::New());
  m_HelperPolyLinesToBePainted->InsertElement( 0, false );
}

mitk::PlanarAngle::~PlanarAngle ( ) [protected, virtual]

Definition at line 35 of file mitkPlanarAngle.cpp.

{
}

Member Function Documentation

void mitk::PlanarAngle::EvaluateFeaturesInternal ( ) [protected, virtual]

Calculates feature quantities of the planar figure.

Implements mitk::PlanarFigure.

Definition at line 169 of file mitkPlanarAngle.cpp.

{
  if ( this->GetNumberOfControlPoints() < 3 )
  {
    // Angle not yet complete.
    return;
  }

  // Calculate angle between lines
  const Point2D &p0 = this->GetControlPoint( 0 );
  const Point2D &p1 = this->GetControlPoint( 1 );
  const Point2D &p2 = this->GetControlPoint( 2 );

  Vector2D v0 = p1 - p0;
  Vector2D v1 = p1 - p2;

  v0.Normalize();
  v1.Normalize();
  double angle = acos( v0 * v1 );

  this->SetQuantity( FEATURE_ID_ANGLE, angle );
}

void mitk::PlanarAngle::GenerateHelperPolyLine	(	double	mmPerDisplayUnit,
		unsigned int	displayHeight
	)		`[protected, virtual]`

Generates the poly-lines that should be drawn the same size regardless of zoom.

Implements mitk::PlanarFigure.

Definition at line 78 of file mitkPlanarAngle.cpp.

References QuadProgPP::t().

{
  // Generate helper-poly-line for angle
  if ( m_ControlPoints->Size() < 3)
  {
    m_HelperPolyLinesToBePainted->SetElement(0, false);
    return; //We do not need to draw an angle as there are no two arms yet
  }
  m_HelperPolyLines->ElementAt( 0 )->Reserve( 3 );
  const Point2D &centerPoint = m_ControlPoints->ElementAt( 1 );
  const Point2D &boundaryPointOne = m_ControlPoints->ElementAt( 0 );
  const Point2D &boundaryPointTwo = m_ControlPoints->ElementAt( 2 );

  double radius = centerPoint.EuclideanDistanceTo( boundaryPointOne );
  if ( radius > centerPoint.EuclideanDistanceTo( boundaryPointTwo ) )
  {
    radius = centerPoint.EuclideanDistanceTo( boundaryPointTwo );
  }

  //Fixed size radius depending on screen size for the angle
  double nonScalingRadius = displayHeight * mmPerDisplayUnit * 0.05;

  if (nonScalingRadius > radius)
  {
    m_HelperPolyLinesToBePainted->SetElement(0, false);
    return; //if the arc has a radius that is longer than the shortest arm it should not be painted
  }

  m_HelperPolyLinesToBePainted->SetElement(0, true);
  radius = nonScalingRadius;

  double angle = this->GetQuantity( FEATURE_ID_ANGLE );

  //Determine from which arm the angle should be drawn

  Vector2D v0 = boundaryPointOne - centerPoint;
  Vector2D v1 = boundaryPointTwo - centerPoint;
  Vector2D v2;
  v2[0] = 1.0;
  v2[1] = 0.0;

  v0[0] = v0[0] * cos( 0.001 ) - v0[1] * sin( 0.001 ); //rotate one arm a bit
  v0[1] = v0[0] * sin( 0.001 ) + v0[1] * cos( 0.001 );
  v0.Normalize();
  v1.Normalize();
  double testAngle = acos( v0 * v1 );
  //if the rotated arm is closer to the other arm than before it is the one from which we start drawing
  //else we start drawing from the other arm (we want to draw in the mathematically positive direction)
  if( angle > testAngle )
  {
    v1[0] = v0[0] * cos( -0.001 ) - v0[1] * sin( -0.001 ); 
    v1[1] = v0[0] * sin( -0.001 ) + v0[1] * cos( -0.001 );

    //We determine if the arm is mathematically forward or backward
    //assuming we rotate between -pi and pi
    if ( acos( v0 * v2 ) > acos ( v1 * v2 ))
    {
      testAngle = acos( v1 * v2 );
    }
    else
    {
      testAngle = -acos( v1 * v2 );
    }
  }
  else
  {
    v0[0] = v1[0] * cos( -0.001 ) - v1[1] * sin( -0.001 ); 
    v0[1] = v1[0] * sin( -0.001 ) + v1[1] * cos( -0.001 );
    //We determine if the arm is mathematically forward or backward
    //assuming we rotate between -pi and pi
    if ( acos( v0 * v2 ) < acos ( v1 * v2 ))
    {
      testAngle = acos( v1 * v2 );
    }
    else
    {
      testAngle = -acos( v1 * v2 );
    }
  }
  // Generate poly-line with 16 segments
  m_HelperPolyLines->ElementAt( 0 )->Reserve( 16 );
  for ( int t = 0; t < 16; ++t )
  {
    double alpha = (double) t * angle / 15.0 + testAngle;

    m_HelperPolyLines->ElementAt( 0 )->ElementAt( t )[0] = centerPoint[0] + radius * cos( alpha );
    m_HelperPolyLines->ElementAt( 0 )->ElementAt( t )[1] = centerPoint[1] + radius * sin( alpha );
  }
}

void mitk::PlanarAngle::GeneratePolyLine ( ) [protected, virtual]

Generates the poly-line representation of the planar figure.

Implements mitk::PlanarFigure.

Definition at line 67 of file mitkPlanarAngle.cpp.

{
  // Generate poly-line for angle
  m_PolyLines->ElementAt( 0 )->Reserve( m_ControlPoints->Size() );

  for ( unsigned int i = 0; i < m_ControlPoints->Size(); ++i )
  {
    m_PolyLines->ElementAt( 0 )->ElementAt( i ) = m_ControlPoints->ElementAt( i );
  }
}

virtual const char* mitk::PlanarAngle::GetClassName ( ) const [virtual]

Reimplemented from mitk::PlanarFigure.

unsigned int mitk::PlanarAngle::GetMaximumNumberOfControlPoints ( ) const [inline, virtual]

Angle has 3 control points per definition.

Implements mitk::PlanarFigure.

Definition at line 60 of file mitkPlanarAngle.h.

  {
    return 3;
  }

unsigned int mitk::PlanarAngle::GetMinimumNumberOfControlPoints ( ) const [inline, virtual]

Place figure in its minimal configuration (a point at least) onto the given 2D geometry.

Must be implemented in sub-classes.Angle has 3 control points per definition.

Implements mitk::PlanarFigure.

Definition at line 53 of file mitkPlanarAngle.h.

  {
    return 3;
  }

static Pointer mitk::PlanarAngle::New ( ) [static]

Referenced by QmitkMeasurement::ActionDrawAngleTriggered(), PlanarFigureIOTestClass::CreatePlanarFigures(), and mitk::PlanarFigureReader::GenerateData().

void mitk::PlanarAngle::PrintSelf	(	std::ostream &	os,
		itk::Indent	indent
	)		const `[protected, virtual]`

Reimplemented from mitk::PlanarFigure.

Definition at line 193 of file mitkPlanarAngle.cpp.

{
  Superclass::PrintSelf( os, indent );
}

Member Data Documentation

const unsigned int mitk::PlanarAngle::FEATURE_ID_ANGLE

Definition at line 40 of file mitkPlanarAngle.h.

Referenced by QmitkPlanarFiguresTableModel::data(), and QmitkMeasurement::PlanarFigureSelectionChanged().

The documentation for this class was generated from the following files:

mitk::PlanarAngle Class Reference

Public Types

Public Member Functions

Static Public Member Functions

Public Attributes

Protected Member Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation